Minimizing Regret with Napkin Algebra

Making architectural decisions is usually the most nerve-wracking part of our job. Outcomes are hard to predict and sometimes there seem to be way too many avenues open to us. Let's look at one such problem and a tool we can use to arrive at a plan.

A cautionary tale?

A common problem in building a site is deciding what compromise to make between flexibility and consistency. A simple WYSIWYG text field on a page can deliver a huge amount of flexibility, at the cost of content that is hard to repurpose and a presentation that can vary wildly from page to page. In contrast, a structured, rigid set of fields can be designed to be presented beautifully and is often very easy to use, but does not allow for content that deviates from this norm.

A compromise between the two approaches is to provide a set of structured "building blocks" that can be assembled in any order to produce complex results. This will sound familiar to many readers because it describes the popular Drupal module Paragraphs. Paragraphs has become a standard tool in our arsenal when building new sites.

In 2014 we architected a project to build landing pages for a site which required exactly this "building block" approach. Paragraphs would be a great fit for this! But Paragraphs was less than a year old at the time, and the project called for content that could interact with many other systems: group membership and content access, moderation, translation, and so forth. There were quirks with these interactions that meant this approach was not viable out of the box.

So a fork in the road presented itself. Do we try to change Paragraphs to fit our needs? Do we develop something new for the site? We did end up doing some custom development for a node-based approach to the problem, and were filled with regret a year or two later when Paragraphs ended up achieving domination and addressing most of the concerns we had at the time.

In the end I'm not sure we can know whether we picked the correct approach—especially given the limited information we had at our disposal—but we can think about the decision process for when similar choices appear in the future.

Let's do some fake math

One way to frame this kind of analysis is a kind of "napkin algebra." We can identify various factors at play and how they interrelate, and use this to shine a light on pros and cons of different solutions.

In this case, we are really trying to minimize the regret we have about our decision. It is likely that if a decision is hard enough, there will always come a time where we wish we had chosen differently, if even for a moment. We can measure this regret R(t) as the cost C_t(t) of the product over its lifetime, adjusted by the anticipated cost C_a and the success S(t) of the result.

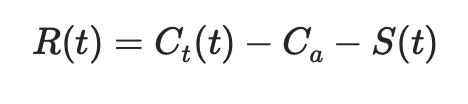
We'll treat C_a as a lump of work done up front, because that is the typical way a project is budgeted, so it is just a simple value. But in reality, cost continues over time. Success is also constantly re-evaluated over time, so it too is expressed as a function here. We can now assess C_t(t) as a combination of initial work, plus time taken for upkeep C_u(x) and fixes C_f(x).

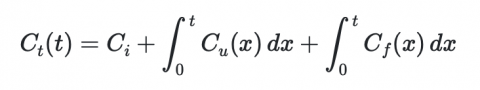
Ooh, look at our fancy integrals! If calculus is lost to the recesses of your mind, we're just saying that we are adding up these cost values from the beginning of the project until time t.

We could make the equations more involved to incorporate other factors, but let's stop here for now. What does this tool do for us? It gives us a way to align various scenarios to see how they affect the variables we are tracking, and how they in turn impact regret.

Scenario 1: Be Lazy

Let's look first at the option of using Paragraphs as-is, ignoring the identified drawbacks and barreling ahead.

C_a doesn't change regardless of our approach. Using an off-the-shelf module that has long-term support means that C_u and C_f can be considered flat, mostly consisting of applying updates as they are released and testing them. C_i will be minimal as well.

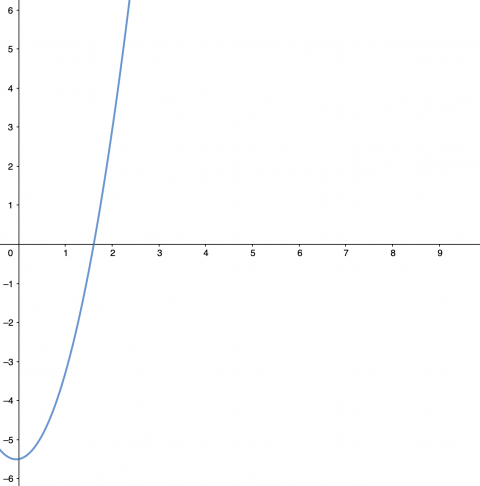
The problem here is S(t). We will launch the feature with a happy client, delivering what seems to be a solid product and under budget. But in a short time, the success metric plummets as the incompatibilities are noticed and spawn new problems. If we are lucky, updates to the project solve these problems; if unlucky they overwhelm the product and we are in a very bad spot. Regret potentially skyrockets.

Scenario 2: Reimplement

What if we build a solution from scratch, then?

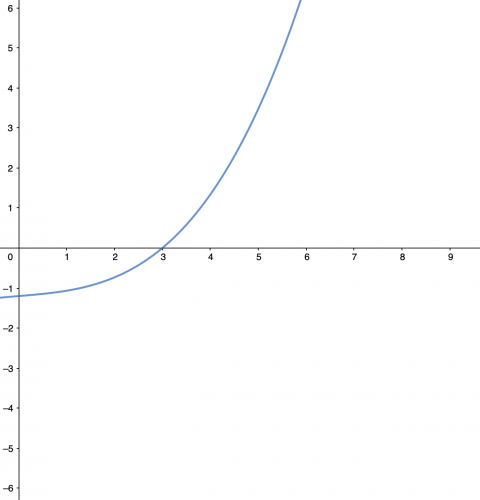
S(t) will decrease over time regardless of the solution, but let's assume we solve the problem well. Since the implementation is specifically tailored to the problem, this value will start high and decrease slowly. C_i is much higher than with an off-the-shelf solution. C_u remains flat and likely lower than the other case, because we won't have a stream of updates that aren't actually applicable to our needs. C_f will begin low but may grow rapidly some years down the road, as requests are made for changes to an aging code base.

The result is a curve that keeps regret low for quite a while, but then quickly becomes something we want to rebuild.

Scenario 3: Patch

To use the off-the-shelf solution but have it actually fit our needs, the solution would be filling the identified gaps and using a patched version of the module, ideally trying to get the patches accepted upstream. We're not modeling the open source part of the problem, but we can see what the cost ramifications of the approach would be.

Starting from scenario 1, we need to adjust the initial cost greatly. Understanding and updating an existing code base always outstrips the effort of a new build. The success curve will be radically different, though, decreasing only slightly over time after a peak nearly as high as scenario 2's. This means that we stave off regret for quite a while, depending mostly on the initial build cost.

Making a decision

Of course, all of these numbers are made up. The conversation about which approach to take is easier, however, since we can align the pros and cons of multiple approaches more easily and visualize their long-term effects. Has napkin algebra ever helped you come to a conclusion?